SVG의 path tag 에 대해 araboja

시작은 SVG에서 호(弧:arc)를 그리는 것에서 비롯하였다.
SVG는 정비율 원인 circle 과 ellipse는 있는데 arc 가 따로 있는 건 아니다.
pie graph 류를 그릴 땐 꼭 필요한데 path 말곤 뾰족한 수가 없어 보인다.

뭐 이렇게 된거 path 에 대해 전부 다 알아보도록 하자.

path는 "명령 숫자 숫자 ..."의 조합인데 각각 의도에 맞는 명령(M,L,H,V,Z,C,S,Q,T,A)와 거기에 맞는 인자들을 잘 넣어서 한방에 그릴 수 있게 한다.
참고로, 각각의 커맨드를 소문자로 쓰면 상대 좌표계로 바뀐다. 인자가 없는 Z의 경우는 어느쪽이던 똑같다.
그냥 생각해봐도 일일이 line 으로 모든 걸 다 그리는 건 비효율적이긴 하다.
어짜피 이런 건 아는 것 보다 "하는" 것이 중요하니까 한번 직접 크롬 개발 환경이라도 열고 해보는 게 좋다.

1. 이동 명령 (M)
2. 직선 명령 (L, H, V)
1. L x y - 현재 점에서 x,y 까지 직선을 긋는다.
2. H x - 현재 점에서 x 위치까지 가로로 직선을 긋는다.
3. V y - 현재 점에서 y 위치까지 세로로 직선을 긋는다.
3. 폐쇄 명령 (Z) - 맨 처음 점으로 되돌아가게끔 직선을 그어 닫힌 면을 만든다.
   인자 없는 것이 특징.
4. 곡선명령 (C,S,Q,T)
1. C x1 y1, x2 y2, x y - 현재 점에서 x,y 까지 직선을 그은 것을 Bezier 곡선을 만든다. 현재 점에서 x1,y1만큼, x,y 에서 x2,y2 만큼 핸들을 사용한다.
   c 즉 상대좌표일 때 주의할 점은 x2 y2는 x,y 기준이 아니라 현재 점 기준.
2. S x2, y2, x y - 이전의 핸들을 연장한다. 아래의 경우를 비교해보자. 둘은 완전히 같은 형태의 곡선을 그리지만 S를 쓰는 쪽이 인자가 하나 적다.
   <path d="M100 500 C 150 400, 200 500, 200 500 C 250 600, 300 500, 300 500"/>
   <path d="M100 600 C 150 500, 200 600, 200 600 S 250 700, 300 600"/>
3. Q x1 y1, x y - C와는 다른 타입(Quadratic curve)이다. 곡선이 x1,y1 점을 지나는 점을 유의하여 보자.
   <path d="M50 600 Q 100 500, 150 600 Q 200 700 250 600"/>
4. T x y - S와 마찬가지로 연장하는 커맨드. Q의 x1 y1을 생략하였다.
   <path d="M50 600 Q 100 500, 150 600 Q 200 700 250 600"/>
   <path d="M50 700 Q 100 600, 150 700 T 250 700"/>
   둘은 완전히 같은 곡선
5. Arc 호
   A rx ry x-axis-rotation large-arc-flag sweep-flag x y
   이거 이야기 하려고 밑밥을 너무 깔았다. C,S,Q,T에 대해선 너무 대충 이야기 한 감이 좀 있는데 사실 나도 잘 모른다. 그어보다 보니 감각적으로 알게된 것은 있는데 정확하게는 수학을 건들지 않고 이야기할 수 없을 것 같다.
   
   여튼 A를 자세히 보아야한다. 이건 Bezier Curve 가 아니다.
1. rx, ry, x, y
   중요한 부분은 rx ry 와 x y는 ellipse 와 완전히 같다.
   rx ry는 분명하다. 가로측 반지름과 세로측 반지름.
   x y가 조금 이상하다 싶은데
   <path d="M 250 100 A 50 50 0 0 0 350 100"></path>
   실제로 그려보면 이런 형태가 된다.
   이전 점인 250,100 에서 출발하여 rx, ry만큼 크기인 호를 350,100까지 그린다.
2. sweep-flag
   여기서 주목해야할 점은 sweep-flag 인데 0 일 경우 반시계 방향 1일 경우 시계 방향으로 그린다.
   즉,
   <path d="M 250 100 A 50 50 0 0 0 350 100"></path>
   <path d="M 250 100 A 50 50 0 0 1 350 100"></path>
   이럴 경우
   <ellipse rx="50" ry="50" cx="300" cy="100" />
   와 완전히 같다.
   원의 중심인 cx, cy 대신 실제 선이 지나가는 위치인 x y를 사용한 점을 주목하자.
3. large-arc-flag
   또 다른 flag 인 large-arc-flag 도 보자.
   만일 호의 일부를 그리기 위해
   <path d="M 400 100 A 50 50 0 0 0 450 150"></path>
   이런 식으로 한다면 어떨까? 400,100 으로부터 50, 50 만큼 떨어진 450, 150 까지 그리는 것이므로 1/4 호를 그릴 수 있다.
   large-arc-flag 를 1로 설정하면 반대 방향으로 크게 돌아 그리는 것을 볼 수 있다.
   마치 팔이 길어서 오른손으로 왼쪽 목을 돌려치는 박진영씨 같은 형국이라고 보면 되겠다.
   
   ...라고 본인은 부인하시긴 하지만 (죄송)
   두 개의 호의 sweepflag 와 large-arc-flag 가 각각 다르기만 하면(0,0 1,1 혹은 0,1 1,0 등) 완전한 원이된다.
4. x-axis-rotation
   이것도 참 미묘하다.
   타원일 경우 x축을 기준으로 n만큼 회전(단위는 degree:각도)한다.
   rotate가 있는데 이걸 쓸 필요가 있나 싶긴 하다.
5. 사실 다 필요없고 이거 한번 보는게 낫다.
   http://codepen.io/lingtalfi/full/yaLWJG/
   x-axis-rotation 이 제대로 작동하는 것을 보기 위해 Radius X와 Radius Y를 다르게 설정하는 것을 추천.

실제로 호를 그리려면 결국 굉장히 암울한데 sin, cos을 이용하여 호의 시작점과 끝점은 미리 알고만 있으면 어떻게든 그릴 수 있긴 하겠다. 그래도 저걸 루프써서 선으로 안긋는게 어딥니다.

사실은 "A 시작각도 끝각도 rx ry cx cy" 였으면 얼마나 좋아 제기랄

http://jsbin.com/rowivid/edit?html,output 같이 하나 열고 연습해보아요.

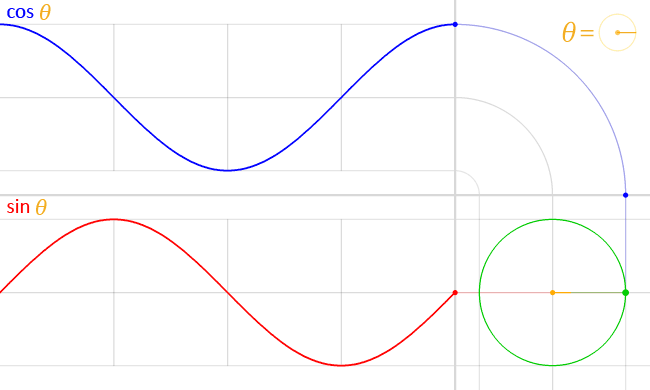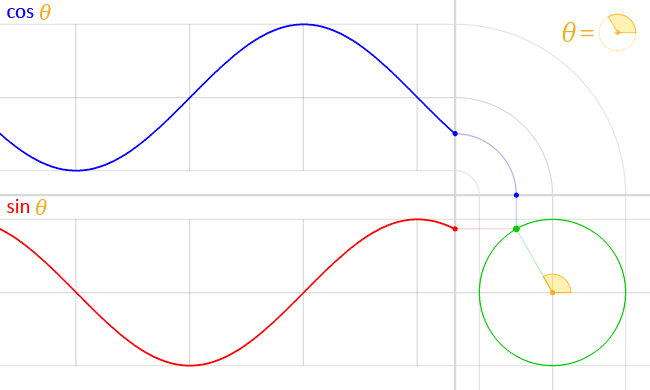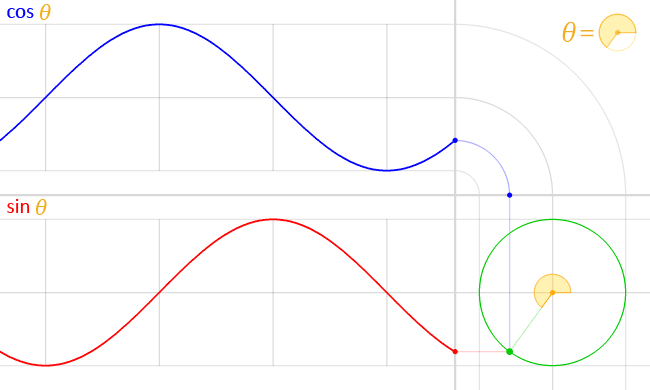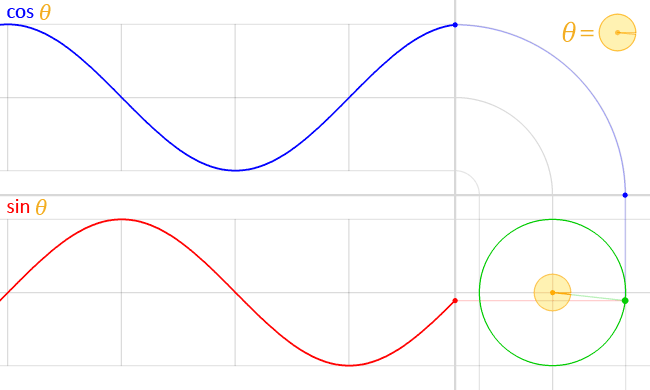
sin, cos으로 원 그리는 건 다들 알고 계시죠?
r 이 반지름, cx,cy가 중심점일 때 degree 각도 만큼인 곳의 점의 위치는
cos(2*Math.PI*degree/360)*r + cx
sin(2*Math.PI*degree/360)*r + cy
이니까 약분하면
[cos(Math.PI*degree/180)*r + cx , sin(Math.PI*degree/180)*r + cy]
으로 x,y를 구할 수 있다. 호의 x,y는 이걸 사용하면 된다.

https://upload.wikimedia.org/wikipedia/commons/3/3b/Circle_cos_sin.gif

중간중간 빵꾸난 지식으로 글 쓰려니 힘들다. 그러니까 여러분도 같이 힘들어요~